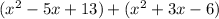Question

Which expression is equivalent to 2x2 - 2x + 7?

- (4x+12) + (2x2–6x+5)
• (x2–5x+13)+(x2 +3X-6)
. (4x? -6x+ 11 ) + (2x² - 4x+4)
(5x® – 8x+120) + (-3x2 + 10x= 13)​

Answer 1

It basically (B) since it’s substituting x=0

Answer 2

B)
`(x^2 - 5x + 13) +(x^2 + 3x - 6)\\`

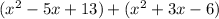
Explanation:

Let's simplify the given options and find the correct answer.

The given expression is
`2x^2 - 2x + 7`

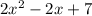
Let's take the option A and simplify.

`-(4x + 12) + (2x^2 - 6x + 5)`

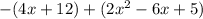
Distributing the negative sign and simplify.

`-4x - 12 + 2x^2 -6x + 5`

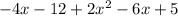
Simplify the like terms.

`2x^2 -10x - 7`

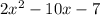
Which is not equal to the given expression.

Let's take the option B and simplify.

`(x^2 - 5x + 13) +(x^2 + 3x - 6)\\`

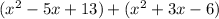
Simplify the like terms, we get

`x^2 + x^2 -5x +3x +13 -6`

`2x^2 -2x +7`

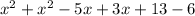
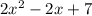
Which is equal to the given expression
`2x^2 -2x +7`

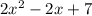
Therefore, the answer is B)
`(x^2 - 5x + 13) +(x^2 + 3x - 6)\\`