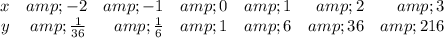The missing parts of the table for
 and
and
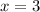 are 1 and 216, respectively.
are 1 and 216, respectively.
Let's solve for the missing values step by step.
The function given is
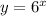 . This means that for each value of
. This means that for each value of
 ,
,
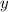 will be
will be
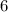 raised to the power of
raised to the power of
 .
.
Step 1: Solve for
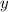 when
when

The exponent law states that any number raised to the power of 0 is 1. Therefore:
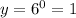
Step 2: Solve for
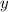 when
when
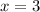
To find
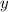 when
when
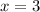 , we simply raise 6 to the power of 3:
, we simply raise 6 to the power of 3:
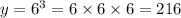
So, the completed table should look like this: