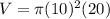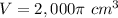Answer:
The exact volume of an oblique cylinder is
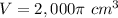
Explanation:
we know that
The Cavalieri's principle states that if two or more figures have the same cross-sectional area at every level and the same height, then the figures have the same volume
so
The volume of the oblique cylinder is equal to

we have


substitute