Question

If y = a + by + c(t)^2 where y = distance , t = time , find the dimension and unit of c.

Please help!!:)​

Answer 1

`\qquad \qquad \bf \huge\star \: \: \large{ \underline{Answer} } \huge \: \: \star`

`\textsf{ \underline{\underline{Steps to solve the problem} }:}`

In the given equation :

`\qquad❖ \: \sf \:y = a + b + c( {t}^(2) )`

If three physical quantities is to be added or subtracted, they must have same dimensions.

So, dimension of y = dimension of c(t²)

And we already know,

• y = M⁰L¹T⁰ [ since it represents distance/length ]

• t = M⁰L⁰T¹ [ since it represents time ]

• t² = M⁰L⁰T²

( by squaring )

Now, we need to calculate dimension and unit of c :

`\qquad❖ \: \sf \:dim(y) = dim(c {t}^(2) )`

`\qquad❖ \: \sf \:M⁰L¹T⁰ = dim(c) \sdot M⁰L⁰T²`

`\qquad❖ \: \sf dim(c) = (M⁰L¹T⁰)/( M⁰L⁰T²)`

`\qquad❖ \: \sf dim(c) = {M⁰L¹T {}^( - 2) }`

Now, we got the dimension of c as :

• M⁰L¹T-²

So, it's SI unit will be :

• m/s²

[ since SI unit of length/distance = m, and SI unit of Time = sec, hence SI unit of T² = s² ]

Answer 2

Question

If y = a + by + c(t)^2 where y = distance , t = time , find the dimension and unit of c.

`\boxed{\green{c=M^0L^1T^(-2)}}`

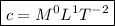
Solution Given:

We know that

Law of Homogeneity of Dimensions In any correct equation representing the relation between physical quantities, the dimensions of all the terms must be the same on both sides.

Dimension of Time is denoted by [T]

Dimension of distance is denoted by [L]

Dimension of mass is denoted by [M]

So,

Dimension of a, by, c(t)^2 should be equal to y.

y=[L] .......[1]

a=[L].......[2]

by=[L].......[3]

c(t)^2=[L].....[4]

Now

The dimension of c can be obtained as:

c(t)^2=[L]

c=
`([L])/([T^2])`

`\boxed{\green{c=M^0L^1T^(-2)}}`

Sry for late!!