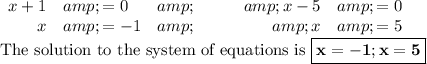Question

Solve the system of equations y=2x-3 y=x^2-2x-8

Answer 1

the solutions to the equations is (-1, -5) and (5, 7)

Answer 2

`\boxed{x = -1; \, x = 5}`

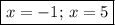
Explanation:

(a) Set the two functions equal to each other

`\begin{array}{rcl}y & = & 2x - 3\\y & = & x^(2) - 2x - 8\\2x - 3 & = & x^(2) - 2x - 8\\2x & = & x^(2) -2x - 5\\x^(2) - 4x - 5 & = & 0\\\end{array}`

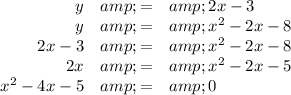
(b) Factor the quadratic equation

Find two numbers that multiply to give -5 and add to give ₄9.

Possible pairs are 1, -5; -1, 5;

By trial and error, you will find that 1 and -5 work:

1 × (-5) = -5 and 1 - 5= -4

x² - 4x - 8 = (x + 1)(x - 5)

(c) Solve the quadratic

`\begin{array}{rlcrl}x+ 1 & =0 & \qquad & x - 5 & =0\\x & = -1 & \qquad & x & = 5\\\end{array}\\\text{The solution to the system of equations is }\boxed{\mathbf{x = -1; x = 5}}`