Which represents the solution(s) of the graphed system of equations, y = x2 + 2x – 3 and y = x – 1? (1, 0) and (0, –1) (–2, –3) and (1, 0) (0, –3) and (1, 0) (–3, –2) and (0, 1)…

Question

asked Mar 3, 2020 225k views

2 Answers

Italankin · Answer 1 · 2020-03-05T00:54:52+0000

ANSWER

The solutions are (-2,-3) and (1,0).

EXPLANATION

The given system has equations:

$y = {x}^(2) + 2x - 3$

and

y = x - 1

We equate both equations:

${x}^(2) + 2x - 3 = x - 1$

${x}^(2) + 2x - x - 3 + 1 = 0$

${x}^(2) + x - 2 = 0$

(x - 1)(x + 2) = 0

This implies that,

$x = - 2 \: or \: x = 1$

When x=-2 , y=-2-1=-3

When x=1, y=1-1=0

The solutions are (-2,-3) and (1,0)

John Kariuki · Answer 2 · 2020-03-09T08:58:38+0000

Answer:

Second option: (-2,-3) and (1,0)

Explanation:

Given the system of equations
$\left \{ {{y = x^2 + 2x-3} \atop {y = x - 1}} \right.$ , you can rewrite them in this form:

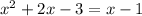
x^2 + 2x-3= x - 1

Simplify:

$x^2 + 2x-3-x+1=0\\\\x^2+x-2=0$

Factor the quadratic equation. Choose two number whose sum be 1 and whose product be -2. These are: 2 and -1, then:

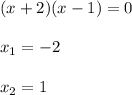
$(x+2)(x-1)=0\\\\x_1=-2\\\\x_2=1$

Substitute each value of "x" into any of the original equation to find the values of "y":

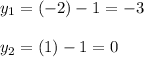
$y_1= (-2) - 1=-3\\\\y_2=(1)-1=0$

Then, the solutions are:

(-2,-3) and (1,0)