Answer:
The initial value of the given geometric sequence is 2.
Explanation:
The given points are (1,2), (2,4) and (3,8).
It means the first term is 2, second term is 4 and third term is 8. So, the common ratio is
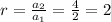
A geometric sequence is defined as

Where, a is first term of the sequence, r is common ratio and n is number of term. In other words f(1) is the initial value of the geometric sequence.
The given geometric sequence is
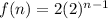
The value of f(1) is 2.
Therefore the initial value of the given geometric sequence is 2.