Question

Which equation has x=4 as the solution? A) ^log 4 (3x+4)=2 B) ^log 3 (2x-5)=2 C) ^log x 64=4 D) ^log x 16=4

Answer 1

(A)

Explanation:

on edg 2021

Answer 2

`\log_(4)(3x + 4) = 2`

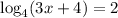
EXPLANATION

Consider the equation:

`\log_(4)(3x + 4) = 2`

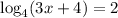
When we rewrite this logarithmic equation in the exponential form, we obtain:

`3x + 4= {4}^(2)`

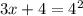
Note that to write a logarithmic equation in exponential form, the base of the logarithm is still the base in the exponential form.

We now simplify the RHS.

`3x + 4 = 16`

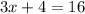
Group like terms

`3x = 16 - 4`

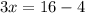
This implies that

`3x = 12`

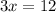
Divide both sides by 3

`(3x)/(3) = (12)/(3)`

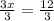
Simplify to get;

`x = 4`

Hence the equation that has x=4 as a solution is

`\log_(4)(3x + 4) = 2`

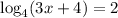
Another way to do this is to substitute x=4 into each equation. The equation that is satisfied is the correct choice.