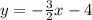Question

What is the equation of the line perpendicular to 2x – 3y = 13 that passes through the point (–6, 5)?

Answer 1

Answer:
`y=-(3)/(2)x-4`

Explanation:

The equation of the line in Slope-intercept form is:

`y=mx+b`

Where "m" is the slope and "b" is the y-intercept.

To express the given equation of the line in this form, we need to solve for "y":

`2x - 3y = 13\\\\-3y=-2x+13\\\\y=(-2)/(-3)x+(13)/(-3)\\\\y=(2)/(3)x-(13)/(3)`

We can identify that the slope of this line is:

`m=(2)/(3)`

Since the slopes of perpendicular lines are negative reciprocals, then the slope of the other line is:

`m=-(3)/(2)`

Now, we need to substitute the given point and the slope into
`y=mx+b` and solve for "b":

`5=-(3)/(2)(-6)+b\\\\5=9+b\\\\5-9=b\\\\b=-4`

Substituting values, we get that the equation of this line is:

`y=-(3)/(2)x-4`

Answer 2

`y =- (3)/(2)x - 4`

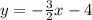
Explanation:

Given equation of line is:

2x-3y=13

We will convert the equation of line in point-slope form to find the slope of the line

Let

m_1 be the slope of the line

So,

2x-3y=13

-3y= -2x+13

Dividing both sides by -3

(-3y)/(-3)=(-2x)/(-3)+13/(-3)

y=(2/3)x-13/3

The co-efficient of x is the slope of the line.

So,

m_1=2/3

Let

m_2 be the slope of second line

As we know that product of slopes of two perpendicular line is -1

m_1 m_2= -1

2/3*m_2= -1

m_2= -1*3/2

m_2= -3/2

So m2 is the slope of the line perpendicular to given line.

The standard equation of a line is

y=mx+b

To find the equation of line through (-6,5), put the point and slope in the given form and solve for b

5= -3/2 (-6)+b

5=18/2+b

5=9+b

b=5-9

b= -4

Putting the values of slope and b, we get

`y =- (3)/(2)x - 4`