Answer:
- 10000 people paid $12.00 each for clubhouse seats and
- 26000 people paid $5.00 each for grandstand seats.
Explanation:
The question is asking for a system of equations, which make explanations easy. :)
Define the variables. Setting
 to the number of clubhouse seats sold and
to the number of clubhouse seats sold and
 to the number of grandstand seats sold will be sufficient. The "let statement[s]" will be:
to the number of grandstand seats sold will be sufficient. The "let statement[s]" will be:
- Let
 be the number of clubhouse seats sold.
be the number of clubhouse seats sold. - Let
 be the number of grandstand seats sold.
be the number of grandstand seats sold.
The number of equations shall be no less than the number of variables for the solution to be unique. There are two variables. It will take at least two equations to find a unique solution.
Everyone at the race need a seat. The number clubhouse seats plus the number of grandstand seats shall be the same as the number people at the race. There were 36,000 people. Therefore the first equation shall be:
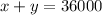 .
.
Every clubhouse seat will add $12.00 to the receipt.
 clubhouse seats will add $
clubhouse seats will add $
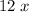 to the receipt. Similarly,
to the receipt. Similarly,
 grandstand seats will add $
grandstand seats will add $
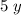 to the receipt. The two values shall add up to $250,000.
to the receipt. The two values shall add up to $250,000.
Drop the dollar sign to get the second equation:
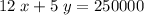 .
.
Hence the system:
![\displaystyle \left\{\begin{aligned}& x + y = 36000 && \textcircled{\raisebox{-0.9pt}1}\\ & 12\;x + 5\;y = 250000 && \textcircled{\raisebox{-0.9pt}2}\end{aligned} \phantom{\small credit for the raisebox hack: tex[dot]stackexchange[dot]com/questions/7032/good-way-to-make-textcircled-numbers}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/8s6brry2lp4zjs5i4hwkk9y3nzx9x7gar1.png) .
.
Solve this system.
The first non-zero coefficient in equation
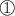 is already one. That's the coefficient for
is already one. That's the coefficient for
 . Use multiples of equation
. Use multiples of equation
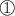 to get rid of
to get rid of
 in other equations (equation
in other equations (equation
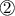 in this case.)
in this case.)
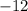 times equation
times equation
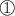 is
is
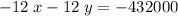 .
.
Add
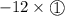 to
to
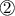 to get:
to get:
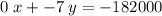 .
.
Divide both sides by -7 to get:
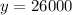 .
.
Add -1 times this equation to equation
 to get:
to get:
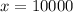 .
.
That is:
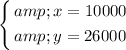 .
.
In other words,
- 10000 clubhouse seats were sold, and
- 26000 grandstand seats were sold.