Question

Felicity set the thermostat in her living room to 68°F. The room temperature t, in degrees Fahrenheit, m minutes after the thermostat is activated, satisfies t = 2cos(0.21m) + 68. Determine the period of the function and explain what it represents. Include the maximum and minimum temperatures in your answer.

Answer 1

Answer with explanation:

Temperature in the living room =68°F

The equation which satisfies ,the room temperature t, in degrees Fahrenheit, m minutes after the thermostat is activated, satisfies

t=2 Cos (0.21 m) +68----------(1)

⇒To determine the period of the function

Z= A cos (sx+q)+r

As period of cos x is 2 π.

So,the given function has period

`=(2\pi)/(s)`

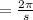
So, the period of function 1, is given by

`=(2\pi)/(0.21)`

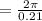
⇒The meaning of period of the function is that after every period of
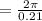`=(2\pi)/(0.21)` the temperature of the room increases or decreases by an integer equal to 2.

⇒Cosine function has maximum value of 1 , and Minimum value of -1.

-1 ≤ Cos x ≤ 1

So, the Maximum value of function = 2 ×1+68°=70°----Maximum Temperature

And, the minimum value of function = 2 ×(- 1)+68°=66°----Minimum Temperature