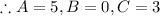Question

The form of the partial fraction decomposition of a rational function is given below.

5x^2+3x+54/(x+3)(x^2+9)=A/x+3+Bx+C/x^2+9

Find A,B,and C

Answer 1

`A=5, B=0,C=3`

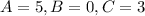
Explanation:

The partial fraction decomposition is given as:

`(5x^2+3x+54)/((x+3)(x^2+9)) \equiv (A)/(x+3)+(Bx+C)/(x^2+9)`

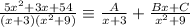
We collect LCD on the RHS to obtain;

`(5x^2+3x+54)/((x+3)(x^2+9)) \equiv (A(x^2+9)+(x+3)(Bx+C))/((x+3)(x^2+9))`

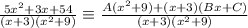
We expand the parenthesis in the numerator of the fraction on the RHS.

`(5x^2+3x+54)/((x+3)(x^2+9)) \equiv (Ax^2+9A+Bx^2+(3B+C)x+3C)/((x+3)(x^2+9))`

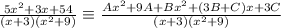
This implies that:

`(5x^2+3x+54)/((x+3)(x^2+9)) \equiv ((A+B)x^2+(3B+C)x+3C+9A)/((x+3)(x^2+9))`

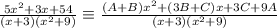
This is now an identity. Since the denominators are equal, the numerators must also be equal.

`5x^2+3x+54=(A+B)x^2+(3B+C)x+3C+9A`

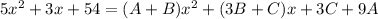
We compare coefficients of the quadratic terms to get:

`A+B=5\implies B=5-A...(1)`

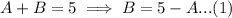
Also the coefficients of the linear terms will give us:

`3B+C=3...(2)`

The constant terms also gives us;

`3C+9A=54...(3)`

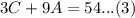
Put equation (1) in to equations (2) and (3).

`3(5-A)+C=3\implies C=3A-12...(4)`

`3C+9A=54...(5)`

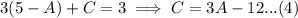
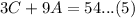
Put equation (4) into (5).

`3(3A-12)+9A=54`

`9A-36+9A=54`

`9A+9A=54+36`

`18A=90`

`A=(90)/(18) =5`

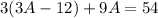
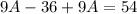
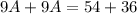
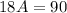
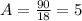
Do backward substitution to get:

`C=3(5)-12=3`

`B=5-5=0`

`\therefore A=5, B=0,C=3`