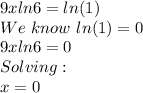Part A: If (6^2)^X = 1, what is the value of x? Explain your answer. (5 points) Part B: If (6^9)^x = 1, what are the possible values of x? Explain your answer.

Question

asked Nov 7, 2020 151k views

1 Answer

Derek Tomes · Answer 1 · 2020-11-14T09:24:03+0000

Answer:

Part A: X=0

Part B: x=0

Explanation:

Part A

(6^2)^X = 1

Applying the exponent rule:
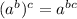
(a^b)^c = a^(bc)

So, our equation will become:

6^(2X) = 1

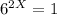
We know if f(x) = g(x) then ln(f(x))= ln(g(x))

SO, taking natural logarithm ln on both sides and solving.

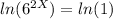
ln(6^(2X)) =ln(1)

We know,
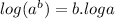log(a^b) = b.loga Applying the rule,

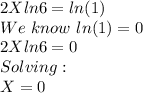
$2Xln6 =ln(1)\\We\,\,know\,\,ln(1)=0\\2Xln6 =0\\Solving:\\X=0$

Part B

(6^9)^x = 1

Applying the exponent rule:
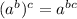
(a^b)^c = a^(bc)

So, our equation will become:

6^(9x) = 1

We know if f(x) = g(x) then ln(f(x))= ln(g(x))

SO, taking natural logarithm ln on both sides and solving.

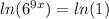
ln(6^(9x)) =ln(1)

We know,
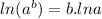ln(a^b) = b.lna Applying the rule,

$9xln6 =ln(1)\\We\,\,know\,\,ln(1)=0\\9xln6 =0\\Solving:\\x=0$