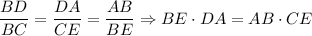Question

Given: Quadrilateral ABCD is inscribed in the circle.

Diagonals AC and BD meet at point E.
AD = CD

Prove: BE X AD = EC X AB​

Answer 1

See explanation

Explanation:

Consider triangles ABD and BEC. In these tirangles:

• Angles BCE and ADB are congruent, because angles BCA and BDA areinscribed angles subtended on the same arc AB;
• Angles CBE and DBA are congruent too. Consider two angles DBA and DCA, they are congruent, because they are inscribed angles subtended on the same arc AD. Since AD=CD, angles ACD and DAC are congruent as angles adjacent to the base of isosceles triangle ACD. Angles DAC and CBD are congruent as inscribed angles subtended on the same arc CD. Hence, ∠DBA=∠DCA=∠DAC=∠CBD. Angle CBD is angle CBE too.

So, by AA similarity theorem, tringles DBA and CBE are similar. Similar triangles have proportional corresponding sides, thus

`(BD)/(BC)=(DA)/(CE)=(AB)/(BE)\Rightarrow BE\cdot DA=AB\cdot CE`