Answer:
first option
(8, -1)
Explanation:
We have the following system of linear equations
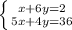
To solve the system multiply the first equation by -5 and then add it to the second equation.
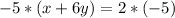
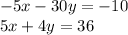
-----------------
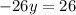
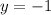
substitute
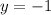 in any of the two equations and then solve for x
in any of the two equations and then solve for x
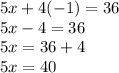
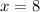
The answer is the first option
(8, -1)