Question

Arrange the expressions in ascending order of their values when x=-2

1-x^2over1-2x
x2-1over1-2x
2x^2+xover2
3x^2+1over2(x-1)

Answer 1

The expressions in ascending order would be:

`(3x^2+1)/(2(x-1)) < (x^2-1)/(1-2x) < (x^2)/(1-2x) < (2x^2+x)/(2)`

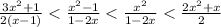
At x = -2

Step-by-step explanation:

First, we will evaluate the given expressions at x = -2

1- The first expression:

`(x^2)/(1-2x)=((-2)^2)/(1-2(-2))=(4)/(5)`

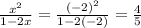
2- The second expression:

`(x^2-1)/(1-2x)=((-2)^2-1)/(1-2(-2))=(3)/(5)`

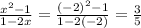
3- The third expression:

`(2x^2+x)/(2)=(2(-2)^2+(-2))/(2)=3`

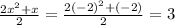
4- The fourth expression:

`(3x^2+1)/(2(x-1))=(3(-2)^2+1)/(2(-2-1))=-(13)/(6)`

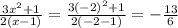
Then, we will arrange the values in an ascending order:

`-(13)/(6) < (3)/(5) < (4)/(5) < 3`

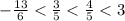
Finally, we arrange the expressions based on the value arrangement:

`(3x^2+1)/(2(x-1)) < (x^2-1)/(1-2x) < (x^2)/(1-2x) < (2x^2+x)/(2)`

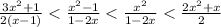
Hope this helps :)