Question

What is the factored form of x^12y^18+1?

Answer 1

`(x^(4)y^(6)+1)(x^(8)y^(12)-x^(4)y^(6)+1)`.

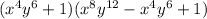Explanation:

We want to expand:
`x^(12)y^(18)+1`.

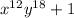We can rewrite this as the sum of two cubes.

`(x^(4))^3(y^(6))^3+1=(x^(4)y^(6))^3+1^3`.

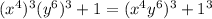Recall and use the sum of cubes identity:
`a^3+b^3=(a+b)(a^2-ab+b^2)`

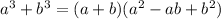
By comparing our newly rewritten expression to this identity, we have
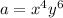`a=x^4y^6` and
`b=1`.

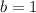We substitute into the identity to get:

`(x^(4)y^(6))^3+1^3=[x^(4)y^(6)+1][(x^(4)y^(6))^2-(x^(4)y^(6))(1)+1^2]`.

We now use this rule of exponents :
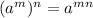`(a^m)^n=a^(mn)` to get;

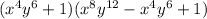`(x^(4)y^(6)+1)(x^(8)y^(12)-x^(4)y^(6)+1)`.