Answer:
Hence, the probability that a randomly selected reference book is a hardcover is:
0.4
Explanation:
Let A denote the event that the book selected is a reference book.
and B denote the event that the book is hardcover.
Let P denote the probability of an event.
We are asked to find:
P(B|A)
We know that:
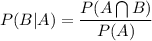
From the table we have:
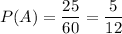
and
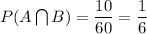
Hence, we have:
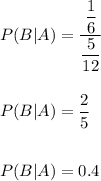
Hence, the answer is:
0.4