Answer:
Explanation:
Let

Subbing in:
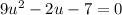
a = 9, b = -2, c = -7
The product of a and c is the aboslute value of -63, so a*c = 63. We need 2 factors of 63 that will add to give us -2. The factors of 63 are {1, 63}, (3, 21}, {7, 9}. It looks like the combination of -9 and +7 will work because -9 + 7 = -2. Plug in accordingly:
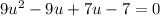
Group together in groups of 2:
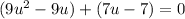
Now factor out what's common within each set of parenthesis:
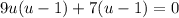
We know this combination "works" because the terms inside the parenthesis are identical. We can now factor those out and what's left goes together in another set of parenthesis:
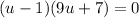
Remember that
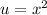
so we sub back in and continue to factor. This was originally a fourth degree polynomial; that means we have 4 solutions.

The first two solutions are found withing the first set of parenthesis and the second two are found in other set of parenthesis. Factoring
 gives us that x = 1 and -1. The other set is a bit more tricky. If
gives us that x = 1 and -1. The other set is a bit more tricky. If
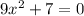 then
then
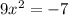 and
and
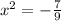
You cannot take the square root of a negative number without allowing for the imaginary component, i, so we do that:
 ±
±
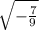
which will simplify down to
 ±
±
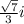
Those are the 4 solutions to the quartic equation.