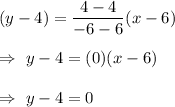Answer:
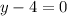
Explanation:
The equation of line passing through two points (a,b) and (c,d) is given by :-
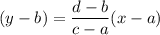
The standard form of equation of a line is given by :-
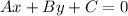 , where A , B , and C are integers.
, where A , B , and C are integers.
Then , the equation of line passing through two points K(6,4) and L(-6,4) is given by :-