Question

Based on the graph how many real number solutions to the equation X^3+6x^2+12x+8=0have

Answer 1

One real root.

Step-by-step explanation

The graph of the function

`f(x) = {x}^(3) + 6{x}^(2) + 12x + 8`

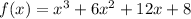
is shown in the attachment.

According to the Fundamental Theorem of Algebra, this function must have 3 roots including real and complex roots.

The x-intercepts gives the number of real roots.

Observe that the graph has only one intercept.

This implies that, the equation:

`{x}^(3) + 6{x}^(2) + 12x + 8 = 0`

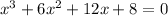
has only one real solution.