Question

Consider the function y = -2-3cos (x+pi). What effect does the -2 have on the basic graph

Answer 1

Vertical Shift Down 2 Units

Explanation:

Answer 2

-2 shift the graph of the basic function down by 2 units.

EXPLANATION

The given cosine function is:

`y = - 2 - 3 \cos(x + \pi)`

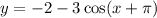
This equation can be rewritten as:

`y = - 3 \cos(x + \pi) + - 2`

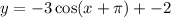
We compare this to

`y = a \cos(bx + c) + d`

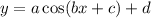
The effect d has on the graph is that, it shifts the graph up by d units.

If d is negative the graph shifts down by d units.

Since d=-2, the graph will shift down by 2 units.