Use the Polynomial Identity below to help you create a list of 10 Pythagorean Triples: (x^(2)+y^(2))^(2)=(x^(2)-y^(2))^(2)+(2xy)^(2) Hint #1: c² = a² + b² Hint #2: pick 2 positi…

Question

Use the Polynomial Identity below to help you create a list of 10 Pythagorean Triples:

(
`x^(2)`+
`y^(2)`)
`^(2)`=(
`x^(2)`-
`y^(2)`)
`^(2)`+(2xy)
`^(2)`
Hint #1: c² = a² + b²
Hint #2: pick 2 positive integers x and y, where x > y

Answer 1

See explanation

Explanation:

You are given the equality

`(x^2+y^2)^2=(x^2-y^2)^2+(2xy)^2`

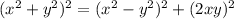
where x, y are two positive integers with x>y.

1. x=2,y=1, then

`c=x^2+y^2=2^2+1^2=5\\ \\a=x^2-y^2=2^2-1^2=3\\ \\b=2xy=2\cdot 2\cdot 1=4`

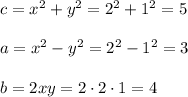
First Pythagorean triple is (3,4,5)

2. x=3,y=1, then

`c=x^2+y^2=3^2+1^2=10\\ \\a=x^2-y^2=3^2-1^2=8\\ \\b=2xy=2\cdot 3\cdot 1=6`

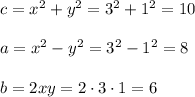
Second Pythagorean triple is (6,8,10)

3. x=3,y=2, then

`c=x^2+y^2=3^2+2^2=13\\ \\a=x^2-y^2=3^2-2^2=5\\ \\b=2xy=2\cdot 3\cdot 2=12`

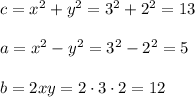
Third Pythagorean triple is (5,12,13)

4. x=4,y=1, then

`c=x^2+y^2=4^2+1^2=17\\ \\a=x^2-y^2=4^2-1^2=15\\ \\b=2xy=2\cdot 4\cdot 1=8`

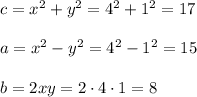
Fourth Pythagorean triple is (8,15,17)

5. x=4,y=2, then

`c=x^2+y^2=4^2+2^2=20\\ \\a=x^2-y^2=4^2-2^2=12\\ \\b=2xy=2\cdot 4\cdot 2=16`

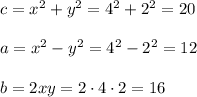
Fifth Pythagorean triple is (12,16,20)

6. x=4,y=3, then

`c=x^2+y^2=4^2+3^2=25\\ \\a=x^2-y^2=4^2-3^2=7\\ \\b=2xy=2\cdot 4\cdot 3=24`

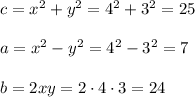
Sixth Pythagorean triple is (7,24,25)

7. x=5,y=1, then

`c=x^2+y^2=5^2+1^2=26\\ \\a=x^2-y^2=5^2-1^2=24\\ \\b=2xy=2\cdot 5\cdot 1=10`

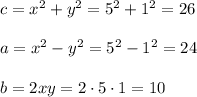
Seventh Pythagorean triple is (10,24,26)

8. x=5,y=2, then

`c=x^2+y^2=5^2+2^2=29\\ \\a=x^2-y^2=5^2-2^2=21\\ \\b=2xy=2\cdot 5\cdot 2=20`

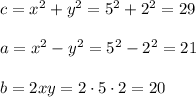
8th Pythagorean triple is (20,21,29)

9. x=5,y=3, then

`c=x^2+y^2=5^2+3^2=34\\ \\a=x^2-y^2=5^2-3^2=16\\ \\b=2xy=2\cdot 5\cdot 3=30`

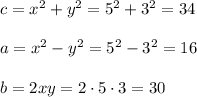
9th Pythagorean triple is (16,30,34)

10. x=5,y=4, then

`c=x^2+y^2=5^2+4^2=41\\ \\a=x^2-y^2=5^2-4^2=9\\ \\b=2xy=2\cdot 5\cdot 4=40`

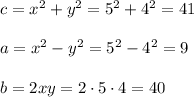
10th Pythagorean triple is (9,40,41)