Question

The graph below represents the solution set of which inequality

Answer 1

B

Explanation:

A. x^2 - 2x - 8 < 0

(x - 4)(x + 2) < 0

B. x^2 + 2x - 8 < 0

(x + 4)(x - 2) < 0

C. x^2 - 2x - 8 > 0

(x - 4)(x - 2) > 0

D. x^2 + 2x - 8 > 0

(x + 4)(x - 2) > 0

Since roots here are -4 and 2, the answer is either B or D.

When you test a point in the interval between -4 and 2, for example 0, it is negative.

So the answer is B.

Answer 2

The answer is
`x^2+2x-8<0`

Explanation:

In order to determine the answer, we have two alternatives:

1. Solving every option and check which is correct.
2. Replacing two or three numbers in every option and check which is correct.

In this case, we use the second option because it is easier to replace a value and solving basic math operations. Also, if we choose a good first value, we will eliminate immediately some options.

We can choose values between -4 and 2. Every time we could choose 0 value, we should do it.

First value:
`x=0`. Replacing:

`-8<0\\-8<0\\-8>0\\-8>0`

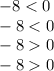
We can see that the two first options are correct, the two last options are wrong.

Second value:
`x=-3`. Replacing:

`(-3)^2-2*(-3)-8<0\\9+6-8<0\\7<0\\\\(-3)^2+2*(-3)-8<0\\9-6-8<0\\-5<0`

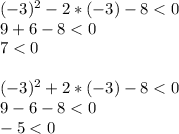
We can see that the first option is wrong.

Finally, the correct option is the second one:

`x^2+2x-8<0`