Question

Which statement is the most appropriate comparison of the spreads

Answer 1

The answer is C

Explanation:

Answer 2

Answer: D. The interquartile range (IQR) for Town A , 15° is less than the interquartile range for town B , 20°.

Explanation:

The interquartile range is most suitable term to compare the spread of two different data displayed by box-whisker plot.

The formula for interquartile range :-

`IQR=Q_3-Q_1`

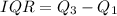
For Town A , First quartile :
`Q_1=15`

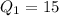
Second quartile :
`Q_2=30`

`IQR=30-15=15`

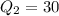
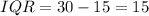
For Town B , First quartile :
`Q_1=20`

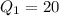
Second quartile :
`Q_2=40`

`IQR=40-20=20`

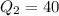
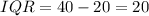
Clearly , the interquartile range (IQR) for Town A , 15° is less than the interquartile range for town B , 20°.