Question

Find the arc length intercepted by a central angle of radians in a circle whose radius is 18.4 inches. 13.8π 15.2π 24.5π

Answer 1

If the measure of the given central angle is
`\theta` rad, then the length of the subtended arc is
`\ell` satisfying

`\frac{\ell}{2\pi(18.4\,\mathrm{in})}=\frac{\theta\,\mathrm{rad}}{2\pi\,\mathrm{rad}}\implies\ell=36.8\pi\theta\,\mathrm{in}`

It's not clear from the question what the value of
`\theta` is...

Answer 2

The arc length is dependent upon the radian measure of central angle.

Explanation:

We are given the following information in the question:

Radius of circle = 18.4 inches

In order to answer this question we need to make the following assumption:

Let the central angle of circle measured as
`\theta\text{radians}`

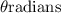
Formula:

`\text{Radian measure of } \theta = \displaystyle(s)/(r)\\\\\text{where s is the arc length and r is the radius of circle.}`

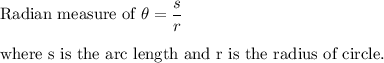
Putting the values:

`\theta = \displaystyle(s)/(18.4)\\\\s = 18.4* \theta \text{ inches}`

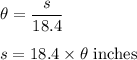
The arc length is dependent upon the radian measure of central angle.