Question

Which could be the function?

The graph shows the axis of symmetry for a quadratic
function f(x)
Of(x) = (x + 4)
O f(x) = x2 + 4
O f(x) = (x -
Of(x) = x2 +4

Answer 1

the answer is c

Explanation:

just took the quiz on E2020

Answer 2

`f(x)=(x-4)^(2)`

Explanation:

we have that

The axis of symmetry shown in the graph is x=4

we know that

The axis of symmetry of a vertical parabola is equal to the x-coordinate of the vertex

so

Verify each case

case a) we have

`f(x)=(x+4)^(2)`

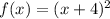
The vertex is the point (-4,0)

therefore

Cannot be the function

case b) we have

`f(x)=x^(2)+4`

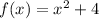
The vertex is the point (0,4)

The axis of symmetry is x=0

therefore

Cannot be the function

case c) we have

`f(x)=(x-4)^(2)`

The vertex is the point (4,0)

The axis of symmetry is x=4

therefore

Could be the function

case d) we have

`f(x)=x^(2)-4`

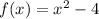
The vertex is the point (0,-4)

The axis of symmetry is x=0

therefore

Cannot be the function