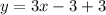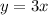ANSWER
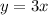
Step-by-step explanation
The given function is
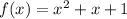
To find the gradient function, we find the first derivative;
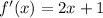
To find the gradient at (1,3), we put x=1 into the gradient function to get;
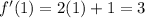
The equation of the tangent line is
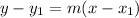
We substitute the point and the slope to get,
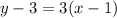
This simplifies to