Question

An ideal gas at a given initial state expands to a fixed final volume. would the work be greater if the expansion occurs at constant pressure or at constant temperature? explain.

Answer 1

Constant pressure

Step-by-step explanation:

At constant pressure,

`w = -p\Delta V = -p(V_(f) - V_(i))`

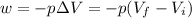
At constant temperature,

`w = -RT \ln \left((V_(f))/(V_(i)) \right)`

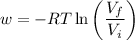
1 mol of an ideal gas at STP has a volume of 22.71 L.

Let's compare the work done as it expands under each condition from an initial volume of 22.71 L.

Isobaric expansion

`w = -100p(V_(2) - 22.71}); \text{(1 bar$\cdot$L = 100 J)}`

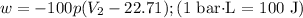
A plot of -w vs V₂ gives a straight line (red) with a constant slope of 100 J/L as in the diagram below (Note that w is work done on the system, so -w is the work done by the system). \

Isothermal expansion

`w= -8.314 * 273.15 \ln \left((V_(f))/(22.71) \right)\\\\= -2271 \left( \ln V_(f) -\ln22.71 \right)\\= -2271 \left(\ln V_(f) - 3.123 \right)\\= 7092 - 2271\ln V_(f)`

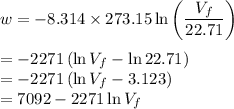
A plot of -w vs V₂ is a logarithmic curve. Its slope starts at 100 J/mol but decreases as the volume increases (the blue curve below).

Thus, the work done during an expansion at constant pressure is greater than if the system is at constant temperature.