Answer:
D) 20 feet by 20 feet
Explanation:
Given:
The area of the original grass lawn reduced by 8 feet on each side.
The smaller lawn's area = 144 square feet which is represented by the equation
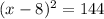 , where "x" is the side of the original lawn.
, where "x" is the side of the original lawn.
To find the original dimension of the lawn, we need to solve for x from the above equation.
To solve follow the steps.
Step 1:
To get rid of square on the right hand side, we need to take square root on both sides.
Taking the square root on both sides, we get
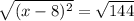

Step 2:
Now add 8 on both sides, we get
x - 8 + 8 = 12 + 8
x = 20
Therefore, the original dimensions of the lawn is 20 feet by 20 feet.