Question

What transformation was not done to the linear parent function, f(x)=x, to get the function g(x)=-3(x-4)-7

A. Reflection over the x-axis
B. Shift down 7 units
C. Shift right 4 units
D. Horizontal stretch by a factor of 3

Answer 1

Answer: D. Horizontal stretch by a factor of 3.

Explanation:

Below are some transformations for a function
`f(x)`:

If
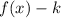`f(x)-k`, then it is shifted "k" units down.

If
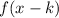`f(x-k)`, then it is shifted rigth"k" units.

If
`-f(x)`, then it is reflected across the x-axis.

If
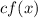`cf(x)` and
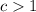`c>1`, then it is stretched vertically by a factor of "c".

If
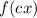`f(cx)` and
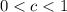`0<c<1`, then it is stretched horizontally by a factor of
`(1)/(c)`.

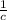Based on this, the transformations done to the function
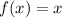`f(x)=x` to get the function
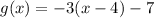`g(x)=-3(x-4)-7` are:

- It is shifted 7 units down.

- It is shifted rigth 4 units.

- It is reflected over the x-axis.

- It is vertically stretched by a factor of 3.

Therefore, the transformations that was not done to the function
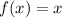`f(x)=x` to get the function
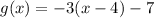`g(x)=-3(x-4)-7` is:

Horizontal stretch by a factor of 3.