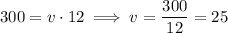Question

A train travels 300km at a constant speed of V km/h. If the train had travelled 5km/h faster, the journey would have taken two hours less. Find the speed of the train travelling at the slower speed.

Answer 1

The original equation states that

`300=vt`

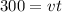
We make the same distance, with higher speed, in less time:

`300=(v+5)(t-2)`

Comparing the two equations, we deduce

`vt = (v+5)(t-2) = vt-2v+5t-10 \iff -2v+5t-10=0 \iff v = (5t-10)/(2)`

If we substitute this expression for v in the first equation, we have

`300=\left((5t-10)/(2)\right)t=(5t^2-10t)/(2)`

We deduce

`5t^2-10t=600 \iff t^2-2t-120=0`

whose solutions are

`t=-10,\quad t=12`

We can only accept the positive solution, so we have t=12. Substitute this again in the first equation:

`300=v\cdot 12 \implies v = (300)/(12) = 25`