Answer:
16. Angle C is approximately 13.0 degrees.
17. The length of segment BC is approximately 45.0.
18. Angle B is approximately 26.0 degrees.
15. The length of segment DF "e" is approximately 12.9.
Explanation:
16
By the law of sine, the sine of interior angles of a triangle are proportional to the length of the side opposite to that angle.
For triangle ABC:
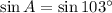 ,
,- The opposite side of angle A
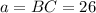 ,
, - The angle C is to be found, and
- The length of the side opposite to angle C
 .
.
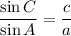 .
.
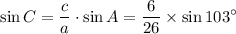 .
.
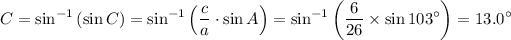 .
.
Note that the inverse sine function here
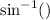 is also known as arcsin.
is also known as arcsin.
17
By the law of cosine,
 ,
,
where
 ,
,
 , and
, and
 are the lengths of sides of triangle ABC, and
are the lengths of sides of triangle ABC, and
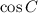 is the cosine of angle C.
is the cosine of angle C.
For triangle ABC:
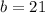 ,
,
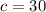 ,
, - The length of
 (segment BC) is to be found, and
(segment BC) is to be found, and - The cosine of angle A is
 .
.
Therefore, replace C in the equation with A, and the law of cosine will become:
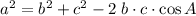 .
.
 .
.
18
For triangle ABC:
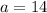 ,
,
 ,
,
 , and
, and- Angle B is to be found.
Start by finding the cosine of angle B. Apply the law of cosine.
 .
.
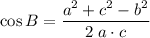 .
.
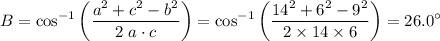 .
.
15
For triangle DEF:
- The length of segment DF is to be found,
- The length of segment EF is 9,
- The sine of angle E is
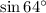 , and
, and - The sine of angle D is
 .
.
Apply the law of sine:
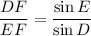
 .
.