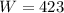Answer:
Washer: 423
Dryer: 350
Explanation:
Since the washer and dryer cost is unknown at the moment, let's just represent the washer cost as the variable "W", and the dryer cost as the variable "D".
Since the combined cost is 773, we can set up the following equation:
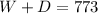
Since the washer costs 73 more than the dryer, this means that:
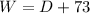
Since we're just solving a systems of equations, we can use the second equation, which represents the value of "W" in terms of the variable "D". We can use this representation to substitute it into the first equation and solve for "D"
Original Equation:
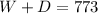
Substitute in D+73 for W
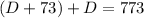
Combine like terms:
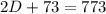
Subtract 73 from both sides:
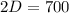
Divide both sides by 2
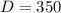
Now we can plug this value into either the first or second equation we made to solve for the value of "W", but we can just use the first equation since it's much easier:
Original Equation:
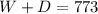
Substitute 350 as D

Subtract 350 from both sides: