Question

Help with those three please!!

Answer 1

Part 1) Option A. The axis of symmetry is x=4

Part 2) Option C. minimum

Part 3) Option A. (4,-4)

Part 4) Option B. (2,0) and (6,0)

Explanation:

we have

`f(x)=x^(2)-8x+12`

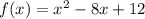
Part 1) What is the axis of symmetry of the parabola described by the equation above?

we know that

The equation above is a vertical parabola open upward

The axis of symmetry is the x-coordinate of the vertex

Find the vertex of the parabola (convert the equation in vertex form)

`f(x)-12=x^(2)-8x`

`f(x)-12+16=x^(2)-8x+16`

`f(x)+4=x^(2)-8x+16`

`f(x)+4=(x-4)^(2)`

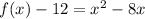
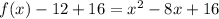
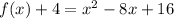
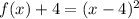
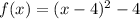`f(x)=(x-4)^(2)-4` ----> equation in vertex form

The vertex of the parabola is (4,-4)

so

The axis of symmetry is x=4

Part 2) The vertex of the equation above is also

we know that

The equation above is a vertical parabola open upward

therefore

The vertex is a minimum

Part 3) What is the vertex of the parabola described by the equation above

we know that

The equation of the parabola into vertex form is equal to

`f(x)=(x-4)^(2)-4`

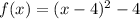
therefore

The vertex of the parabola is (4,-4)

Part 4) What are the x-intercepts of the parabola described by the equation above

we know that

The x-intercepts are the values of x when the value of y is equal to zero

so

`f(x)+4=(x-4)^(2)`

f)x)=0

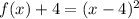
so

`4=(x-4)^(2)`

take square root both sides

`(x-4)=(+/-)2`

`x=4(+/-)2`

`x=4(+)2=6`

`x=4(-)2=2`

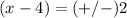
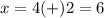
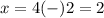
therefore

The x-intercepts are

(2,0) and (6,0)