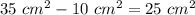Answer:
The area of triangle ABC is
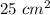
Explanation:
we know that
The area of triangle ABC is equal to the area of triangle ABO minus the area of triangle ACO
see the attached figure to better understand the problem
step 1
Find the area of triangle ABO
The area is equal to
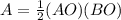
substitute values
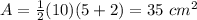
step 2
Find the area of triangle ACO
The area is equal to
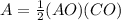
substitute values
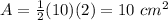
step 3
Find the area of triangle ABC