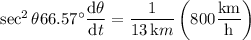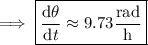The rocket's altitude
 at time
at time
 is
is
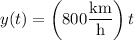
so that after
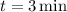 , it will have traveled
, it will have traveled
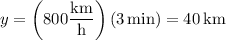
The angle of elevation
 at time
at time
 is such that
is such that
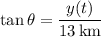
At the moment when
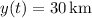 , this angle is
, this angle is
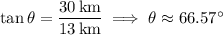
Differentiating both sides of the equation above gives
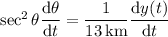
and substituting the angle
 found above, and
found above, and
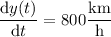 , we get
, we get