Answer:
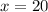 or
or

Explanation:
To solve the quadratic equation we must factor the expression
Look for 2 numbers that when you multiply them, obtain the result -100 and when you add them, obtain the result -15.
You can verify that these numbers are -20 and 5
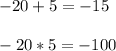
Then the polynomial factors are
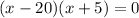
The zero product property says that if two terms
 then
then
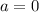 or
or
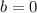
So
 or
or

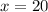 or
or
