Answer:
20. OPTION D.
12. OPTION B.
Explanation:
20. An inverse variaton equation has this form:
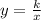
Where "k" is the constant of variation.
If Q varies inversely as the square of p, then the equation is:
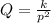
Knowing that
 when
when
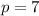 , you can solve for "k" and caculate its value:
, you can solve for "k" and caculate its value:
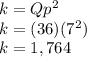
Then, to find the value of "Q" when
 , substitute the known values into
, substitute the known values into
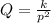 :
:

12. Given
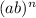 , you get:
, you get:
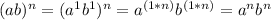
Then:

This matches with the option B.