Answer:
The axis of symmetry for the function f(x) is x=-3.
Explanation:
The vertex form of a quadratic function is
 .... (1)
.... (1)
Where, (h,k) is vertex and x=h is the axis of symmetry.
The given function is
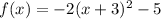 .... (2)
.... (2)
From (1) and (2), we get
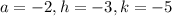
The axis of symmetry is
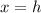
Substitute h=-3 in the above equation.

Therefore the axis of symmetry for the function f(x) is x=-3.