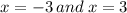Question

Show all work to identify the discontinuity and zero of this function. 3x/x^2-9

Answer 1

Zero(s)

`x = 0`

The function is discontinuous at

`x = - 3 \:and \: x = 3`

Step-by-step explanation

The given rational function is

`y = \frac{3x}{ {x}^(2) - 9 }`

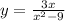
For this function to be equal to zero, then the numerator must be zero.

Equate the numerator to zero and solve for x.

`3x = 0`

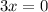
This implies that

`x = (0)/(3) = 0`

The rational function is discontinuous when the denominator is equal to zero.

`{x}^(2) - 9 = 0`

Solve this quadratic equation using the square root method or otherwise.

`{x}^(2) = \pm √(9)`

`{x} = \pm 3`

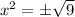
There is discontinuity at

`x = - 3 \:and \: x = 3`