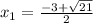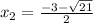Question

Select the two values of x that are roots of this equation x^2+3x-3=0
Apex

Answer 1

C, and D are both roots of this equation

Answer 2

The two values of x that are roots are:

`x_(1) = (-3 + √(21) )/(2)`

`x_(2) = (-3 - √(21) )/(2)`

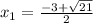
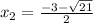
Explanation:

A cuadratic function has the form
`ax^(2) + bx +c = 0`

To calculate the roots of the cuadratic equation
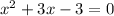`x^(2) + 3x -3 = 0` you have to solve the formula:

`x = (-b)/(2a)` ±
`\frac{\sqrt{b^(2) -4ac} }{2a}`

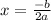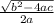
In this case, a =1, b=3 and c= -3

Replacing the values of a,b and c in the formula:

`x = (-3)/((2)(1))` ±
`\frac{\sqrt{(3)^(2) - (4)(1)(-3) } }{(2)(1)}`

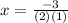Solving the mathematic operations:

x =
`(-3)/(2)` ±
`(√(9 + 12 ) )/(2)`

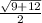
The two roots are:

`x_(1) = (-3 + √(21) )/(2)`

`x_(2) = (-3 - √(21) )/(2)`