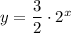Question

write the equation for the exponential function that goes through the points (-2, 0.375) and (7, 192)

Answer 1

`y=(3)/(2)\cdot 2^x`

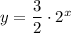
Explanation:

The general equation of the exponential function is

`y=a\cdot b^x`

If the graph of the exponential function passes through the points (-2, 0.375) and (7, 192), then their coordinates satisfy the equation:

`0.375=a\cdot b^(-2)\\ \\192=a\cdot b^7`

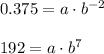
Divide the second equation by the first:

`(192)/(0.375)=(a\cdot b^7)/(a\cdot b^(-2))=(b^7)/(b^(-2))\\ \\512=b^9\\ \\b=\sqrt[9]{512}=2`

Substitute it into the second equation:

`192=a\cdot 2^7\\ \\192=a\cdot 128\\ \\a=(192)/(128)=(96)/(64)=(48)/(32)=(6)/(4)=(3)/(2)`

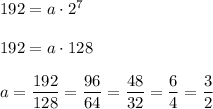
So, the equation of the exponential function is

`y=(3)/(2)\cdot 2^x`