Question

On in-line skates, Bradley skates 4 miles in 20 minutes. At this speed, how long would it take him to skate the entire length of a 12-mile bike path?

Answer 1

Answer: 60 minuites

Step-by-step explanation: actully the dude thats on top of me its only 60 mins not 1hr and 60 mins

Answer 2

1 hour (60 minutes)

Explanation:

If his speed remains the same, that means that this is a linear relationship. y increases at the same rate as x increases. Direct variation and all of that. Because this is a linear relationship, it can be solved using proportions. Set up the given info in a ratio with miles on the top and minutes on the bottom:

`(miles)/(minutes):(4)/(20)`

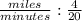
Now we want to know how long (unknown number of minutes) it will take him to go 12 miles. Keep miles with miles and minutes with minutes:

`(miles)/(minutes):(4)/(20)`=
`(12)/(x)`

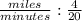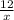
We can cross multiply now to get 4x = 12(20) and 4x = 240. That means that x=60. It will take him 60 minutes (1 hour) to go 12 miles.