Answer:
37.0
Explanation:
You have a total of 3 triangles in one here. Triangle ABC, triangle ABD, and triangle DBC. If we can find out the length of side BD in triangle DBC that will help us later. We have angle D and side DC and we are looking for the hypotenuse of that right triangle DBC. The trig ratio that relates the side adjacent to the reference angle to the hypotenuse is the cosine:
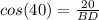
Solving for BD:
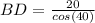
That gives us that BD = 26.1
Now that we know that, we can move into the obtuse triangle that shares the side BD with the right triangle. We have that angle BDC is 40 degrees, and since angle ADB is supplementary to angle BDC, then angle ADB measures 180 - 40 = 140. So angle A is 30, angle ADB is 140, so that means that angle ABD is 10. Because triangle ABD is obtuse and not right you cannot use Pythagorean's Theorem. But you can use the Law of Sines. Set it up like this:
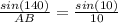
Solve for side AB:

In degree mode on your calculator you'll find that side AB is 37.0