Question

The human eye can respond to as little as 10^-18J of light energy. For a wavelength at the peak of visual sensitivity, 550 nm, how many photons lead to an observable flash?

Answer 1

Approximately 3 photons

Step-by-step explanation:

The energy of a photon at the peak of visual sensitivity is given by:

`E=(hc)/(\lambda)`

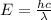
where

h is the Planck constant

c is the speed of light

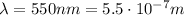`\lambda=550 nm = 5.5\cdot 10^(-7)m` is the wavelength of the photon

Substituting into the formula,

`E_1=((6.63\cdot 10^(-34) Js)(3\cdot 10^( m/s))/(5.50\cdot 10^(-7) m)=3.6\cdot 10^(-19) J`

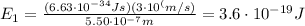
This is the energy of one photon. The human eye can detect an amount of energy of

`E=10^(-18) J`

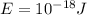
So the amount of photons contained in this energy is

`n=(E)/(E_1)=(10^(-18) J)/(3.6\cdot 10^(-19)J)=2.8 \sim 3`

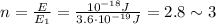
so approximately 3 photons.