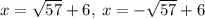Question

Diego is solving the equation x^2-12x = 21

Answer 1

The solutions to the quadratic equations will be:

`x=√(57)+6,\:x=-√(57)+6`

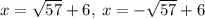
Explanation:

Given the expression

`x^2-12x\:=\:21`

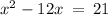
Let us solve the equation by completing the square

`x^2-12x\:=\:21`

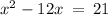
Add (-6)² to both sides

`x^2-12x+\left(-6\right)^2=21+\left(-6\right)^2`

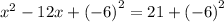
simplify

`x^2-12x+\left(-6\right)^2=57`

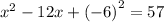
Apply perfect square formula: (a-b)² = a²-2ab+b²

i.e.

`x^2-12x+\left(-6\right)^2=\left(x-6\right)^2`

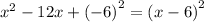
so the expression becomes

`\left(x-6\right)^2=57`

`\mathrm{For\:}f^2\left(x\right)=a\mathrm{\:the\:solutions\:are\:}f\left(x\right)=√(a),\:-√(a)`

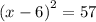
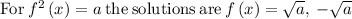
solve

`x-6=√(57)`

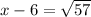
add 6 to both sides

`x-6+6=√(57)+6`

Simplify

`x=√(57)+6`

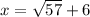
also solving

`x-6=-√(57)`

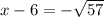
add 6 to both sides

`x-6+6=-√(57)+6`

Simplify

`x=-√(57)+6`

Therefore, the solutions to the quadratic equation will be:

`x=√(57)+6,\:x=-√(57)+6`