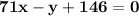Explanation:
The point-slope of an equation of a line:

m - slope
We have the slope m = 71 and the point (-2, 4).
Substitute:
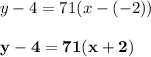
The slope-intercept form of an equation of a line:

Convert:
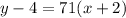 use the distributive property
use the distributive property
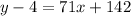 add 4 to both sides
add 4 to both sides

The standard form of an equation of a line:

Convert:
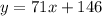 subtract 71x from both sides
subtract 71x from both sides
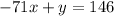 change the signs
change the signs
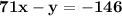
The general form of an equation of a line:
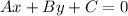
Convert:
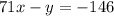 add 146 to both sides
add 146 to both sides