Answer:
A right triangle
Explanation:
Suppose a, b, c are the sides of a triangle,
If a² = b² + c² or b² = a² + c² or c² = a² + b²
Then the triangle is called a right angled triangle,
If a² + b² > c², a² + c² > b², b² + c² > a²
Then the triangle is called an acute triangle,
If a = b = c
Then the triangle is called an equilateral triangle,
If a² + b² < c², where c is the largest side of the triangle,
Then the triangle is called an obtuse triangle,
Now, In triangle RST,
By the distance formula,
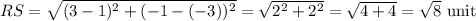
Similarly,
ST = √40 unit,
TR = √32 units,
Since, ST² = RS² + TR²
Hence, by the above explanation it is clear that,
Triangle RST is a right angled triangle,
First option is correct.