Question

The height (in feet) of a rocket launched from the ground is given by the function f(t) = -16t2 + 160t. Match each value of time elapsed (in seconds) after the rocket’s launch to the rocket's corresponding instantaneous velocity (in feet/second).

t = 2 96 t = 3 -64 t = 4 32 t = 5 0 t = 6 -128 t = 7 -32 t = 8 t = 9

Answer 1

t = 2 s= 96

t = 3 s = 64

t = 4 s= 32

t= 5 s = 0

t= 6 s = -32

t = 7 s = -64

t = 8 s = -96

t= 9 s = -128

Explanation:

We have the equation of the position of the rocket as a function of time t.

`f(t) = -16t^2 + 160t`

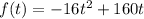
The instantaneous velocity of the rocket as a function of time is given by the derivation of the position with respect to time.

So

`S(t)=(df(t))/(dt) = -2*16t + 160\\\\S(t) = -32t+160`

`s(1) = -32(1)+160=128\ ft/s\\\\s(2) = -32(2)+160=96\ ft/s\\\\s(3) = -32(3)+160=64\ m/s\\\\s(4) = -32(4)+160=32\ m/s\\\\s(5) = -32(5)+160=0\ m/s\\\\s(6) = -32(6)+160=-32\ m/s\\\\s(7) = -32(7)+160=-64\ m/s\\\\s(8) = -32(8)+160=-96\ m/s\\\\s(9) = -32(9)+160=-128\ m/s`

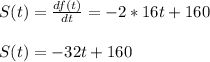
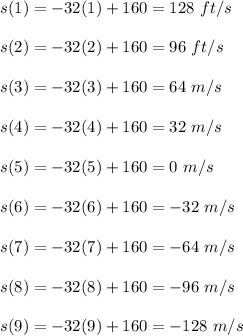
So

t = 2 s= 96

t = 3 s = 64

t = 4 s= 32

t= 5 s = 0

t= 6 s = -32

t = 7 s = -64

t = 8 s = -96

t= 9 s = -128